입문자를 위한 컴퓨터 이야기 #01 : 동전놀이로 보는 2진법

글을 시작하기 전에

컴퓨터와 관련한 업무나 직업을 준비하는 사람이라면, 공부를 하는 과정에서 컴퓨터에 대해 어려움을 많이 느끼실 수 있을 것 같다는 생각이 듭니다.

제 과거와 경험에 비추어 본다면 기존의 암기 및 주입식 위주의 학습 방식에서 벗어나지 않게 복잡한 용어, 단어, 개념이 등장하고 이를 뇌리에 주입하기 위해 외우고 있기 때문이 아닐까 하는 생각이 들기 때문입니다.

사실 저는 컴퓨터와 관련된 대부분의 지식이 팔 할(80%) 이상이 독학이고, 이 과정에서 저만의 기준으로 스스로 이해하기 쉽게 변형해서 흡수해 오다 보니 기존의 컴퓨터 교육과 관련한 사용법, 이해법, 표현 등 여러 방면에 있어 다소 차이가 있을 수 있습니다. 하지만 이러한 저의 방식이 기존의 컴퓨터 교육법과 맞지 않는 분들 중 누군가에게는 도움이 될 것 같아 이렇게 글을 통해 지식과 경험을 나누는 자리를 마련하게 되었습니다.

따라서 제가 이러한 교육 컨텐츠들 작성하게 된 계기는 다음과 같습니다.

• 재능의 유무와 상관 없이도 컴퓨터를 배울 수 있다 말하고 싶었습니다.
• 재정적 여유가 없으나 스스로 컴퓨터에 대해 배우고 싶은 사람이 있다면 제 경험과 지식을 공개하여 비용과 상관없는 학습의 기회를 제공하고 싶었습니다.
• 기존의 교육 방식이 맞지 않는 분들에게 제 이해와 경험이 도움이 되었으면 했습니다.
• 위와 같은 이유로 학습을 진행하는 과정에서 대중의 분들에게는 간단한 개념만 알아도 되니 컴퓨터라는 대상에 대해 깊게 알아야 한다고, 암기해야만 한다는 부담 갖지 말라 전하고 싶었습니다.
• 즉, 수포자(수학을 포기한 이들) 및 영포자(영어를 포기한 이들)도 컴퓨터에 대해 학습하고 관련 직종에서 일할 수 있다는 메시지를 전하고 싶었습니다.

자, 그럼 여러가지 다룰 이야기가 많이 있겠지만 너무 길어지면 집중력이 떨어질 것이기에 내용을 시작하면서 부담스럽지 않게 간단하게 몇 가지만 이야기로 다뤄보도록 하겠습니다.

컴퓨터는 "계산"에서 시작되는 것 아세요?

컴퓨터(Computer) 라는 말은 원래 라틴어 computare 에서 유래했다고 합니다. 함께를 의미하는 com- 과 계산하다, 세다 라는 뜻을 가진 putare 단어의 합성어에서 출발해서 본래의 의미는 "함께 계산하다" 또는 "계산하는 사람" 이라는 뜻을 가졌다고 해요.

요컨데 이전까지는 인간 컴퓨터(Human Computer) 즉, 사람들이 계산을 대신했고 20세기 중반 무렵부터 기계가 사람을 대신해서 계산하는 것이 보편화 되면서 컴퓨터(Computer)라는 단어의 의미가 계산하는 기계로 변화했다고 보면 되겠습니다.

사실 일반적인 경우에 여러분들은 자세하고 부담스럽게 달달달 외우는 것이 아니라 간단하게 이런 것이 있었다 맥락만 알아도 됩니다. 자신이 컴퓨터와 관련된 박사 학위를 노릴 뿐만 아니라 역사나 그 외 더 자세한 부분까지 학습하고 연구하는 사람이 될 것이 아니라면, 그리고 그러한 부담으로 인해 학습 진행이 잘 되지 않는다면 구태여 자세히 알 필요는 없습니다. 더 자세한 내용을 연구하고 기록을 남기는 것은 그러한 역할을 하고자 하는 분들께 맡기면 되고, 어느 정도 친해지고 이해가 되었을 때 추가로 찾아보면서 스스로의 지식을 다져나가면 되기 때문입니다.

앞으로도 간간히 컴퓨터와 관련한 예시를 언급하는 과정에서 몇 번 이야기 할 기회가 생기겠지만, 일반인들이 등에서 전구를 갈 때에는 전구의 소켓 크기와 돌려 빼고 끼는 방법만 알면 되지 필라멘트를 어떻게 만들고 저항에 따른 밝기가 어떠하고, 저항과 밝기에 따라 열이 얼마나 발생하며 이를 위해 충전재는 무엇을 써야 하는지 등에 대해선 알 필요가 없기 때문입니다.

우리가 생각해볼 필요가 있는 부분은 컴퓨터의 발전 과정에서 현재의 컴퓨터 구조가 만들어지기까지 채용 된 핵심적인 요소들에 대해서 어떻게 이해하고 받아들일지에 관한 부분 입니다.

세상 모든 것을 0과 1로 표현할 수 있다면? - 2진법의 등장

17세기 독일의 수학자 라이프니츠는 중국 베이징에 있는 프랑스 전도사 부베 신부와 편지를 주고 받는 과정에서 주역[중국 주(周)나라때 만든 역경(易經)]의 8괘를 접하고 현대 컴퓨터의 베이스가 된 2진법을 만들게 되었다고 전해집니다.

주역에서는 '한 일(一)' 모양을 '양', 그리고 이 모양에서 가운데가 끊어진 모양(- -)을 '음'이라고 하고 이 두 가지를 다양하게 짝지어 8괘를 만들고 이걸 다시 64괘로 늘려 사물의 변화를 예측하고 불행을 점쳤는데, 이러한 표기 체계가 라이프니츠에게 자극이 되어 음을 0 으로 양을 1로 하여 두 가지 숫자만으로 세상의 모든 수를 표현할 수 있도록 한 것이 바로 2진법이 등장하게 된 배경이 된 것이죠.

하지만 이쯤되면 이미 이 글을 읽는 분들이 슬슬 "무슨 소리 하고 있나?" "내가 이해를 못한건가?" "0과 1로 모든 숫자를 표현 한다는게 무슨 말이야?" 하고 슬슬 거리두기를 실천하시려는 분들이 생길 것 입니다. 이해합니다.

그래서 우리는 쉽게 이해하면 됩니다. 쉽게.

우리에게 친숙한 놀이를 하나 가져와 보겠습니다. 동전 던지기를 생각해봅시다. 동전이 1개 있습니다. 우리는 통상 이걸 튕겨서 감싸 쥐고 맞추기를 합니다. 자, 우리가 맞출 수 있는 경우의 수는 몇 가지 일까요? 두 가지 경우 뿐입니다. 앞면이거나 뒷면 둘 중 하나 인 것이죠.

이번에는 변화를 하나 줘 볼까요? 동전 2개를 던져서 맞춰보면 우리가 맞출 수 있는 경우의 수는 몇 가지 일까요? 앞면+앞면, 앞면+뒷면, 뒷면+앞면, 뒷면+뒷면으로 네 가지를 나타낼 수 있습니다.

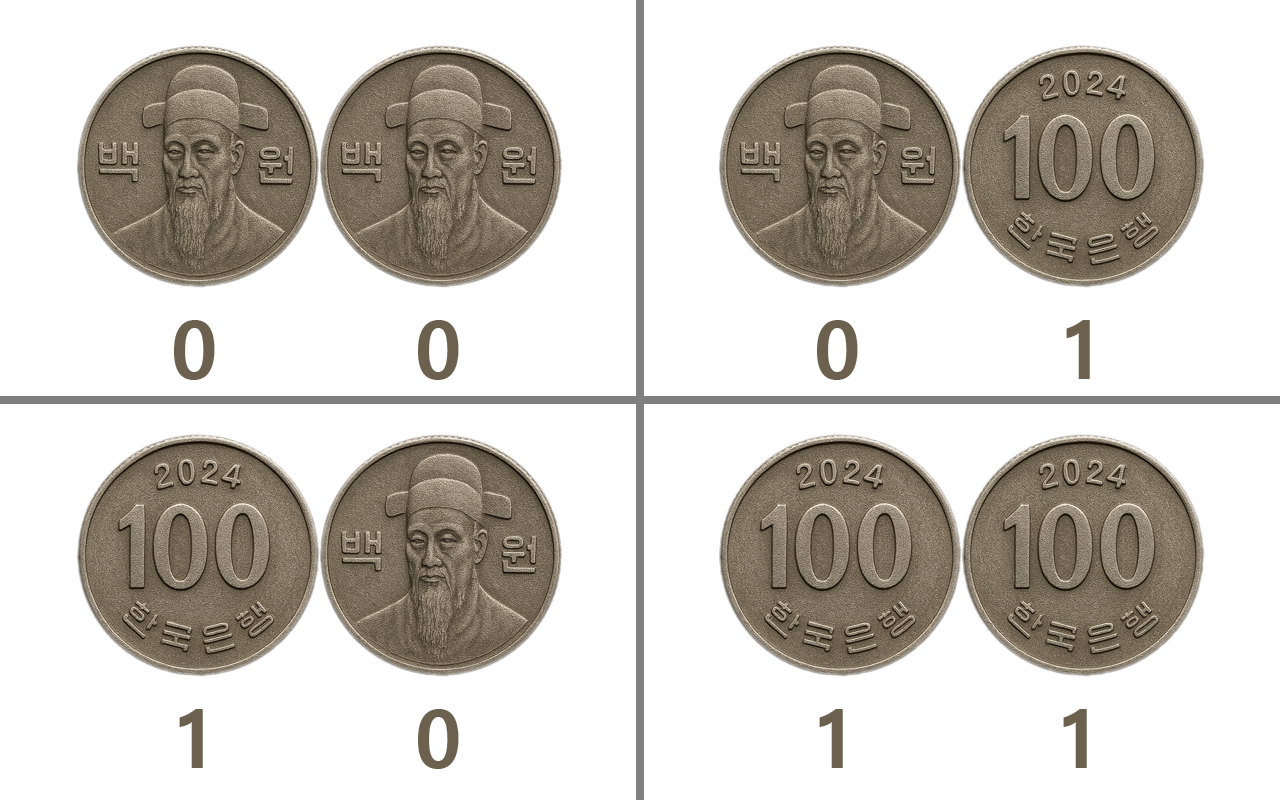
자, 동전의 앞면을 1로 가정하고 동전의 뒷면을 0으로 가정할 때, 동전이 1개만 있으면 0(뒷면) 또는 1(앞면)로 두 가지 경우를 나타낼 수 있고, 동전이 2개가 되면 00(뒤뒤) 01(뒤앞) 10(앞뒤) 11(앞앞) 로 네 가지를 경우를 나타낼 수 있습니다. 동전이 3개가 되면 어떨까요? 000(뒤뒤뒤) 001(뒤뒤앞) 010(뒤앞뒤) 011(뒤앞앞) 100(앞뒤뒤) 101(앞뒤앞) 110(앞앞뒤) 111(앞앞앞) 로 8가지의 경우의 수를 만들 수 있을 겁니다.

만약 이보다 더 많은 경우의 수가 더 필요하다면 동전을 추가하는 것으로 경우의 수를 만들어낼 수 있고 표현할 수 있을 겁니다.

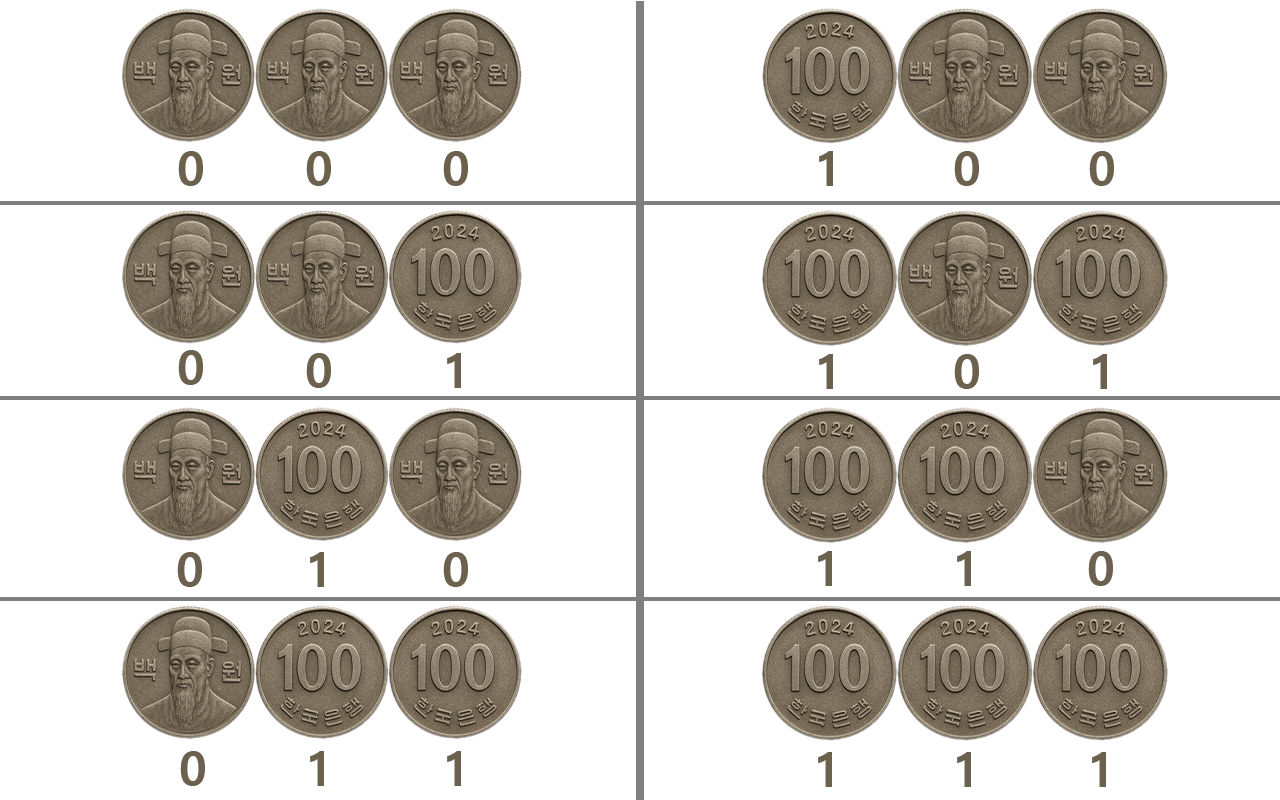
이번에는 동전을 이용해서 좀 다른 가정을 해볼까요? 동전 15개를 이용해서 가로로 3개씩 세로로 5개씩 나열했다고 가정해봅시다. 이제 우리는 이걸로 간단하게 알파벳이나 숫자를 표현할 수도 있을 겁니다.

각각의 동전이 하나의 칸이라고 가정하고, 뒷면은 채워지지 않고 앞면은 채워진 상태라고 보면 A라는 글자가 만들어지는 것을 볼 수 있죠. 위의 이미지를 보면 이해가 쉬울 겁니다.

자 그럼 앞서 동전으로 8가지의 경우의 수를 만든 것을 이용해 우리가 숫자를 표현한다면 어떻게 정리해서 볼 수 있을까요?

어떤가요? 동전의 앞면과 뒷면을 이용해 0 과 1이라는 상태 값으로 가정하고 살펴보니 2개의 상태를 이용해서 숫자를 표현할 수 있었는데, 이렇게 경우의 수를 정리하고 표현하는 방법을 정의해서 다루는 것이 바로 2진법을 이용한 계산이 되는 것이죠.

반면, 표현하는 방법을 3x5로 바꾸어 눈으로 보기 쉽게 표현한 방법은 우리가 모니터 등 화면을 통해서 보는 방법의 기본이 되는 방식이라 이해하면 조금은 쉽게 2진법이 왜 나오는지 생각해보고 조금은 이해할 수 있을 겁니다.

우리의 입문자들은 이렇게 이해하면서 접근해 가면 됩니다. 처음부터 너무 복잡하게 부담스럽게 받아들일 필요가 없습니다. 더 자세하고 깊은 내용은 나중에 조금 더 수준 있는 내용을 다루게 될 때 다시 접하면서 복습도 하고 이해해 나가면 좋겠죠.

참고자료

When Computers Were Human - NASA

What’s often not known is that all the early rocket experiments and later missions to the moon and beyond wouldn’t have been possible without a team at JPL

NASAAnthony Greicius